> import numpy as np
> x = np.arange(24)
> print(x.shape) # prints (24,)
> x = x.reshape( (3,2,4) )
> print(x.shape) # prints (3,2,4)
> x
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7]],

       [[ 8,  9, 10, 11],
        [12, 13, 14, 15]],

       [[16, 17, 18, 19],
        [20, 21, 22, 23]]])

In the numpy array above, there are 3 axes. The first axis, axis=0, has a dimension of 3. The second, axis=1, has a dimension of 2. The third, axis=2, has a dimension of 4. When you specify axis=0 as an argument to one of numpy’s methods, you are telling numpy to operate along this axis.

But what does it means to operate along an axis? As you can see from the diagram below, if we’re operating along axis=0, simply visit 1 element at a time along this axis. In this case, we need to find the mean along axis=0, so we use the 3 elements we’ve gathered from visiting along axis=0 and find their mean.

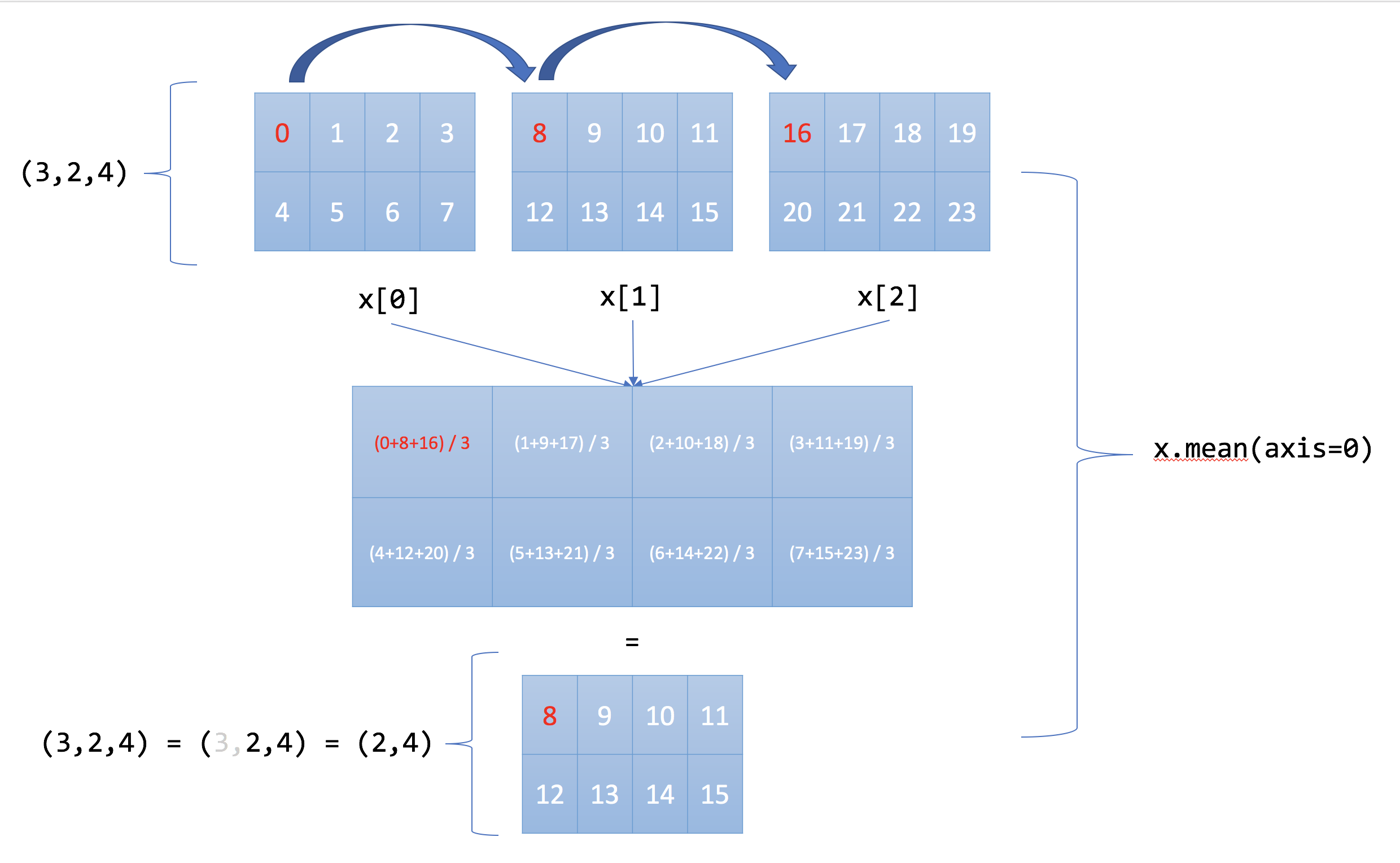
The other way to understand this is if you specify axis=0, you’re telling numpy to make that axis disappear in the resulting numpy array. So if you start out with a (3,2,4) array, you want to get a (2,4) array. To do this, visualize that a (3,2,4) array is the same as three (2,4) arrays. Then combine all three of those (2,4) arrays with the specified operation. In the diagram above, the three arrays are combined to produce a mean.

Numpy Padding

To pad a 2D numpy matrix with zeroes, np.pad(a, [(1,1),(1,1)], 'constant', constant_values=[(0,0),(0,0)]). This takes in a 2x2 matrix of 1’s, and puts 1 layer of 0s all around it.

Let’s break down this line of code. In the first array of [(1,1), (1,1)], each tuple corresponds to one axis in the 2x2 matrix. Let’s call the matrix’s first axis, the x-axis, and the second axis, the y-axis. The first tuple, (1,1), says “add a single value before the first value in the x-axis, and add a single value after the last value in the y-axis.” The second tuple, (1,1), says “add a single value before the first value in the y-axis, and add a single value after the last value in the y-axis.” Now the question is, what values should be added? This is what the third and fourth arguments tell us. The third argument says, “whatever value you add, make sure it’s a constant value”. The fourth argument is similar in structure to the second argument. The first and second tuples correspond with the x- and y-axes, respectively. They say, “add 0 before the first value of the x-axis, and add 0 after the last value of the x-axis.” The same logic applies to the y-axis.